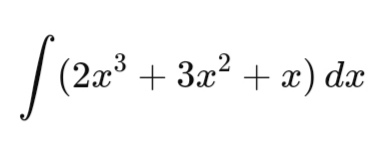Pengertian Integral
Dalam matematika, integral adalah salah satu konsep utama dalam kalkulus, selain turunan. Integral dapat diartikan sebagai operasi kebalikan dari turunan, namun secara umum integral digunakan untuk menghitung luas daerah di bawah kurva, volume benda yang diputar, atau total perubahan berdasarkan suatu laju perubahan. Integral juga digunakan untuk menemukan fungsi asli (antiturunan) dari suatu fungsi turunan.
Ada dua jenis integral:

Rumus Integral

Contoh Soal Integral
Penerapan Integral dalam Kehidupan Sehari-hari
- Menghitung Luas di Bawah Kurva: Integral sering digunakan untuk menghitung luas suatu daerah di bawah kurva. Misalnya, jika Anda memiliki grafik kecepatan terhadap waktu, integral dari kurva ini akan memberi Anda jarak yang telah ditempuh.
- Penghitungan Volume Benda Putar: Integral digunakan untuk menghitung volume benda yang diputar di sekitar sumbu tertentu. Contoh penerapannya adalah dalam industri manufaktur, di mana bentuk-bentuk benda kompleks dapat diukur volumenya dengan menggunakan integral.
- Ekonomi: Dalam ekonomi, integral digunakan untuk menghitung pendapatan total atau biaya total berdasarkan fungsi laju perubahan, seperti pendapatan marjinal atau biaya marjinal.
- Fisika: Integral digunakan dalam hukum gerak, khususnya dalam menghitung jarak yang ditempuh oleh suatu objek berdasarkan laju (kecepatan) yang berubah-ubah seiring waktu. Misalnya, integral digunakan untuk menghitung perpindahan suatu benda berdasarkan grafik kecepatan terhadap waktu.
- Arsitektur dan Desain: Dalam desain struktur yang melibatkan bentuk-bentuk melengkung atau geometri kompleks, integral digunakan untuk menghitung luas atau volume, sehingga material yang tepat dapat dihitung secara efisien.
- Penghitungan Probabilitas: Dalam teori probabilitas, integral digunakan untuk menghitung peluang pada distribusi probabilitas kontinu, seperti dalam menghitung probabilitas kumulatif suatu variabel acak.
Kesimpulan:
Integral adalah alat penting dalam matematika yang digunakan untuk menghitung luas, volume, dan total perubahan dalam berbagai konteks. Penerapannya mencakup banyak aspek kehidupan sehari-hari, dari fisika dan ekonomi hingga arsitektur dan desain. Pemahaman tentang integral memudahkan kita untuk menyelesaikan berbagai masalah yang melibatkan perubahan dan akumulasi.